Computational Statistics And Statistical Modelling

• A1.13

  Computational Statistics and Statistical Modelling

  Part II, 2001

  (i) Assume that the $n$-dimensional observation vector $Y$ may be written as

  $$Y=X \beta+\epsilon$$

  where $X$ is a given $n \times p$ matrix of $\operatorname{rank} p, \beta$ is an unknown vector, and

  $$\epsilon \sim N_{n}\left(0, \sigma^{2} I\right)$$

  Let $Q(\beta)=(Y-X \beta)^{T}(Y-X \beta)$. Find $\widehat{\beta}$, the least-squares estimator of $\beta$, and show that

  $$Q(\widehat{\beta})=Y^{T}(I-H) Y$$

  where $H$ is a matrix that you should define.

  (ii) Show that $\sum_{i} H_{i i}=p$. Show further for the special case of

  $$Y_{i}=\beta_{1}+\beta_{2} x_{i}+\beta_{3} z_{i}+\epsilon_{i}, \quad 1 \leqslant i \leqslant n$$

  where $\Sigma x_{i}=0, \Sigma z_{i}=0$, that

  $$H=\frac{1}{n} \mathbf{1 1}{ }^{T}+a x x^{T}+b\left(x z^{T}+z x^{T}\right)+c z z^{T} ;$$

  here, $\mathbf{1}$ is a vector of which every element is one, and $a, b, c$, are constants that you should derive.

  Hence show that, if $\widehat{Y}=X \widehat{\beta}$ is the vector of fitted values, then

  $$\frac{1}{\sigma^{2}} \operatorname{var}\left(\widehat{Y}_{i}\right)=\frac{1}{n}+a x_{i}^{2}+2 b x_{i} z_{i}+c z_{i}^{2}, \quad 1 \leqslant i \leqslant n .$$

  comment

• A2.12

  Computational Statistics and Statistical Modelling

  Part II, 2001

  (i) Suppose that $Y_{1}, \ldots, Y_{n}$ are independent random variables, and that $Y_{i}$ has probability density function

  $$f\left(y_{i} \mid \theta_{i}, \phi\right)=\exp \left[\left(y_{i} \theta_{i}-b\left(\theta_{i}\right)\right) / \phi+c\left(y_{i}, \phi\right)\right]$$

  Assume that $E\left(Y_{i}\right)=\mu_{i}$, and that $g\left(\mu_{i}\right)=\beta^{T} x_{i}$, where $g(\cdot)$ is a known 'link' function, $x_{1}, \ldots, x_{n}$ are known covariates, and $\beta$ is an unknown vector. Show that

  $$\mathbb{E}\left(Y_{i}\right)=b^{\prime}\left(\theta_{i}\right), \operatorname{var}\left(Y_{i}\right)=\phi b^{\prime \prime}\left(\theta_{i}\right)=V_{i} \text {, say, }$$

  and hence

  $$\frac{\partial l}{\partial \beta}=\sum_{i=1}^{n} \frac{\left(y_{i}-\mu_{i}\right) x_{i}}{g^{\prime}\left(\mu_{i}\right) V_{i}}, \text { where } l=l(\beta, \phi) \text { is the log-likelihood. }$$

  (ii) The table below shows the number of train miles (in millions) and the number of collisions involving British Rail passenger trains between 1970 and 1984 . Give a detailed interpretation of the $R$ output that is shown under this table:

  $\begin{array}{llll} & \text { year } & \text { collisions } & \text { miles } \\ 1 & 1970 & 3 & 281 \\ 2 & 1971 & 6 & 276 \\ 3 & 1972 & 4 & 268 \\ 4 & 1973 & 7 & 269 \\ 5 & 1974 & 6 & 281 \\ 6 & 1975 & 2 & 271 \\ 7 & 1976 & 2 & 265 \\ 8 & 1977 & 4 & 264 \\ 9 & 1978 & 1 & 267 \\ 10 & 1979 & 7 & 265 \\ 11 & 1980 & 3 & 267 \\ 12 & 1981 & 5 & 260 \\ 13 & 1982 & 6 & 231 \\ 14 & 1983 & 1 & 249\end{array}$

  Call:

  glm(formula $=$ collisions $\sim$ year $+\log ($ miles $)$, family $=$ poisson)

  Coefficients:

  $\begin{array}{lrrrr} & \text { Estimate } & \text { Std. Error } & \text { z value } & \operatorname{Pr}(>|z|) \\ \text { (Intercept) } & 127.14453 & 121.37796 & 1.048 & 0.295 \\ \text { year } & -0.05398 & 0.05175 & -1.043 & 0.297 \\ \log \text { (miles) } & -3.41654 & 4.18616 & -0.816 & 0.414\end{array}$

  (Dispersion parameter for poisson family taken to be 1)

  Null deviance: $15.937$ on 13 degrees of freedom

  Residual deviance: $14.843$ on 11 degrees of freedom

  Number of Fisher Scoring iterations: 4

  Part II

  comment

• A4.14

  Computational Statistics and Statistical Modelling

  Part II, 2001

  (i) Assume that independent observations $Y_{1}, \ldots, Y_{n}$ are such that

  $$Y_{i} \sim \operatorname{Binomial}\left(t_{i}, \pi_{i}\right), \log \frac{\pi_{i}}{1-\pi_{i}}=\beta^{T} x_{i} \quad \text { for } 1 \leqslant i \leqslant n$$

  where $x_{1}, \ldots, x_{n}$ are given covariates. Discuss carefully how to estimate $\beta$, and how to test that the model fits.

  (ii) Carmichael et al. (1989) collected data on the numbers of 5 -year old children with "dmft", i.e. with 5 or more decayed, missing or filled teeth, classified by social class, and by whether or not their tap water was fluoridated or non-fluoridated. The numbers of such children with dmft, and the total numbers, are given in the table below:

  \begin{tabular}{l|ll} Social Class & Fluoridated & Non-fluoridated \ \hline I & $12 / 117$ & $12 / 56$ \ II & $26 / 170$ & $48 / 146$ \ III & $11 / 52$ & $29 / 64$ \ Unclassified & $24 / 118$ & $49 / 104$ \end{tabular}

  A (slightly edited) version of the $R$ output is given below. Explain carefully what model is being fitted, whether it does actually fit, and what the parameter estimates and Std. Errors are telling you. (You may assume that the factors SClass (social class) and Fl (with/without) have been correctly set up.)

  

  $\begin{array}{lrrrr} & \text { Estimate } & \text { Std. } & \text { Error } & \text { z value } \\ \text { (Intercept) } & -2.2716 & 0.2396 & -9.480 \\ \text { SClassII } & 0.5099 & 0.2628 & 1.940 \\ \text { SClassIII } & 0.9857 & 0.3021 & 3.262 \\ \text { SClassUnc } & 1.0020 & 0.2684 & 3.734 \\ \text { Flwithout } & 1.0813 & 0.1694 & 6.383\end{array}$

  

  Here 'Yes' is the vector of numbers with dmft, taking values $12,12, \ldots, 24,49$, 'Total' is the vector of Total in each category, taking values $117,56, \ldots, 118,104$, and SClass, Fl are the factors corresponding to Social class and Fluoride status, defined in the obvious way.

  comment

• A1.13

  Computational Statistics and Statistical Modelling

  Part II, 2002

  (i) Suppose $Y_{1}, \ldots, Y_{n}$ are independent Poisson variables, and

  $$\mathbb{E}\left(Y_{i}\right)=\mu_{i}, \log \mu_{i}=\alpha+\beta^{T} x_{i}, 1 \leqslant i \leqslant n$$

  where $\alpha, \beta$ are unknown parameters, and $x_{1}, \ldots, x_{n}$ are given covariates, each of dimension $p$. Obtain the maximum-likelihood equations for $\alpha, \beta$, and explain briefly how you would check the validity of this model.

  (ii) The data below show $y_{1}, \ldots, y_{33}$, which are the monthly accident counts on a major US highway for each of the 12 months of 1970 , then for each of the 12 months of 1971 , and finally for the first 9 months of 1972 . The data-set is followed by the (slightly edited) $R$ output. You may assume that the factors 'Year' and 'month' have been set up in the appropriate fashion. Give a careful interpretation of this $R$ output, and explain (a) how you would derive the corresponding standardised residuals, and (b) how you would predict the number of accidents in October 1972 .

  $\begin{array}{llllllllllll}52 & 37 & 49 & 29 & 31 & 32 & 28 & 34 & 32 & 39 & 50 & 63 \\ 35 & 22 & 27 & 27 & 34 & 23 & 42 & 30 & 36 & 56 & 48 & 40 \\ 33 & 26 & 31 & 25 & 23 & 20 & 25 & 20 & 36 & & & \end{array}$

  $>$ first.glm $-\operatorname{glm}(\mathrm{y} \sim$ Year $+$ month, poisson $) ;$ summary(first.glm $)$

  Call:

  $\operatorname{glm}($ formula $=\mathrm{y} \sim$ Year $+$ month, family $=$ poisson $)$

  \begin{tabular}{lrlll} Coefficients: & & & & \ (Intercept) & Estimate & Std. Error & \multicolumn{1}{l}{ z value } & $\operatorname{Pr}(>|z|)$ \ Year1971 & $-0.81969$ & $0.09896$ & $38.600$ & $<2 e-16$ \ Year1972 & $-0.28794$ & $0.08267$ & $-3.483$ & $0.000496$ \ month2 & $-0.34484$ & $0.14176$ & $-2.433$ & $0.014994$ \ month3 & $-0.11466$ & $0.13296$ & $-0.862$ & $0.388459$ \ month4 & $-0.39304$ & $0.14380$ & $-2.733$ & $0.006271$ \ month5 & $-0.31015$ & $0.14034$ & $-2.210$ & $0.027108$ \ month6 & $-0.47000$ & $0.14719$ & $-3.193$ & $0.001408$ \ month7 & $-0.23361$ & $0.13732$ & $-1.701$ & $0.088889$ \ month8 & $-0.35667$ & $0.14226$ & $-2.507$ & $0.012168$ \ month9 & $-0.14310$ & $0.13397$ & $-1.068$ & $0.285444$ \ month10 & $0.10167$ & $0.13903$ & $0.731$ & $0.464628$ \ month11 & $0.13276$ & $0.13788$ & $0.963$ & $0.335639$ \ month12 & $0.18252$ & $0.13607$ & $1.341$ & $0.179812$ \end{tabular}

  Signif. codes: 0 (, $0.001$ (, $0.01$ (, $0.05$ '.

  (Dispersion parameter for poisson family taken to be 1 )

  $\begin{array}{rlll}\text { Null deviance: } & 101.143 & \text { on } 32 \text { degrees of freedom } \\ \text { Residual deviance: } & 27.273 & \text { on } 19 \text { degrees of freedom }\end{array}$

  Number of Fisher Scoring iterations: 3

  comment

• A2.12

  Computational Statistics and Statistical Modelling

  Part II, 2002

  (i) Suppose that the random variable $Y$ has density function of the form

  $$f(y \mid \theta, \phi)=\exp \left[\frac{y \theta-b(\theta)}{\phi}+c(y, \phi)\right]$$

  where $\phi>0$. Show that $Y$ has expectation $b^{\prime}(\theta)$ and variance $\phi b^{\prime \prime}(\theta)$.

  (ii) Suppose now that $Y_{1}, \ldots, Y_{n}$ are independent negative exponential variables, with $Y_{i}$ having density function $f\left(y_{i} \mid \mu_{i}\right)=\frac{1}{\mu_{i}} e^{-y_{i} / \mu_{i}}$ for $y_{i}>0$. Suppose further that $g\left(\mu_{i}\right)=\beta^{T} x_{i}$ for $1 \leqslant i \leqslant n$, where $g(\cdot)$ is a known 'link' function, and $x_{1}, \ldots, x_{n}$ are given covariate vectors, each of dimension $p$. Discuss carefully the problem of finding $\hat{\beta}$, the maximum-likelihood estimator of $\beta$, firstly for the case $g\left(\mu_{i}\right)=1 / \mu_{i}$, and secondly for the case $g(\mu)=\log \mu_{i}$; in both cases you should state the large-sample distribution of $\hat{\beta}$.

  [Any standard theorems used need not be proved.]

  comment

• A4.14

  Computational Statistics and Statistical Modelling

  Part II, 2002

  Assume that the $n$-dimensional observation vector $Y$ may be written as $Y=X \beta+\epsilon$, where $X$ is a given $n \times p$ matrix of rank $p, \beta$ is an unknown vector, with $\beta^{T}=\left(\beta_{1}, \ldots, \beta_{p}\right)$, and

  $$\epsilon \sim N_{n}\left(0, \sigma^{2} I\right)$$

  where $\sigma^{2}$ is unknown. Find $\hat{\beta}$, the least-squares estimator of $\beta$, and describe (without proof) how you would test

  $$H_{0}: \beta_{\nu}=0$$

  for a given $\nu$.

  Indicate briefly two plots that you could use as a check of the assumption $(*)$.

  Continued opposite Sulphur dioxide is one of the major air pollutants. A data-set presented by Sokal and Rohlf (1981) was collected on 41 US cities in 1969-71, corresponding to the following variables:

  $Y=$ sulphur dioxide content of air in micrograms per cubic metre

  $X 1=$ average annual temperature in degrees Fahrenheit

  $X 2$ = number of manufacturing enterprises employing 20 or more workers

  $X 3=$ population size (1970 census) in thousands

  $X 4=$ average annual wind speed in miles per hour

  $X 5=$ average annual precipitation in inches

  $X 6=$ average annual of days with precipitation per year $.$

  Interpret the $R$ output that follows below, quoting any standard theorems that you need to use.

  $$\begin{aligned} &>\text { next. } \operatorname{lm}-\operatorname{lm}(\log (\mathrm{Y}) \sim \mathrm{X} 1+\mathrm{X} 2+\mathrm{X} 3+\mathrm{X} 4+\mathrm{X} 5+\mathrm{X} 6) \\ &>\text { summary }(\text { next.lm }) \\ &\text { Call: } \operatorname{lm}(\text { formula }=\log (\mathrm{Y}) \sim \mathrm{X} 1+\mathrm{X} 2+\mathrm{X} 3+\mathrm{X} 4+\mathrm{X} 5+\mathrm{X} 6) \end{aligned}$$

  $$\begin{aligned} & \text { Call: } \operatorname{lm}(\text { formula }=\log (\mathrm{Y}) \sim \mathrm{X} 1+\mathrm{X} 2+\mathrm{X} 3+\mathrm{X} 4+\mathrm{X} 5+\mathrm{X} 6) \end{aligned}$$

  Residuals :

  $$\begin{array}{rrrrr} \text { Min } & 1 Q & \text { Median } & 3 Q & \text { Max } \\ \hline .79548 & -0.25538 & -0.01968 & 0.28328 & 0.98029 \end{array}$$

  $\begin{array}{lllll}-0.79548 & -0.25538 & -0.01968 & 0.28328 & 0.98029\end{array}$

  $\begin{array}{lrlcll}\text { Coefficients: } & & & & & \\ & \text { Estimate } & \text { Std. Error } & \text { t value } & \operatorname{Pr}(>|t|) & \\ \text { (Intercept) } & 7.2532456 & 1.4483686 & 5.008 & 1.68 \mathrm{e}-05 & * * * \\ \text { X1 } & -0.0599017 & 0.0190138 & -3.150 & 0.00339 & * * \\ \text { X2 } & 0.0012639 & 0.0004820 & 2.622 & 0.01298 & * \\ \text { X3 } & -0.0007077 & 0.0004632 & -1.528 & 0.13580 & \\ \text { X4 } & -0.1697171 & 0.0555563 & -3.055 & 0.00436 & * * \\ \text { X5 } & 0.0173723 & 0.0111036 & 1.565 & 0.12695 & \\ \text { X6 } & 0.0004347 & 0.0049591 & 0.088 & 0.93066\end{array}$

  Signif. codes: 0 ', $0.001$ ', $0.01$ ', $0.05$ ':

  Residual standard error: $0.448$ on 34 degrees of freedom

  Multiple R-Squared: $0.6541$

  F-statistic: $10.72$ on 6 and 34 degrees of freedom, p-value: $1.126 \mathrm{e}-06$

  comment

• A1.13

  Computational Statistics and Statistical Modelling

  Part II, 2003

  (i) Suppose $Y_{i}, 1 \leqslant i \leqslant n$, are independent binomial observations, with $Y_{i} \sim B i\left(t_{i}, \pi_{i}\right)$, $1 \leqslant i \leqslant n$, where $t_{1}, \ldots, t_{n}$ are known, and we wish to fit the model

  $$\omega: \log \frac{\pi_{i}}{1-\pi_{i}}=\mu+\beta^{T} x_{i} \quad \text { for each } i$$

  where $x_{1}, \ldots, x_{n}$ are given covariates, each of dimension $p$. Let $\hat{\mu}, \hat{\beta}$ be the maximum likelihood estimators of $\mu, \beta$. Derive equations for $\hat{\mu}, \hat{\beta}$ and state without proof the form of the approximate distribution of $\hat{\beta}$.

  (ii) In 1975 , data were collected on the 3-year survival status of patients suffering from a type of cancer, yielding the following table

  \begin{tabular}{ccrr} & & \multicolumn{2}{c}{ survive? } \ age in years & malignant & yes & no \ under 50 & no & 77 & 10 \ under 50 & yes & 51 & 13 \ $50-69$ & no & 51 & 11 \ $50-69$ & yes & 38 & 20 \ $70+$ & no & 7 & 3 \ $70+$ & yes & 6 & 3 \end{tabular}

  Here the second column represents whether the initial tumour was not malignant or was malignant.

  Let $Y_{i j}$ be the number surviving, for age group $i$ and malignancy status $j$, for $i=1,2,3$ and $j=1,2$, and let $t_{i j}$ be the corresponding total number. Thus $Y_{11}=77$, $t_{11}=87$. Assume $Y_{i j} \sim B i\left(t_{i j}, \pi_{i j}\right), 1 \leqslant i \leqslant 3,1 \leqslant j \leqslant 2$. The results from fitting the model

  $$\log \left(\pi_{i j} /\left(1-\pi_{i j}\right)\right)=\mu+\alpha_{i}+\beta_{j}$$

  with $\alpha_{1}=0, \beta_{1}=0$ give $\hat{\beta}_{2}=-0.7328(\mathrm{se}=0.2985)$, and deviance $=0.4941$. What do you conclude?

  Why do we take $\alpha_{1}=0, \beta_{1}=0$ in the model?

  What "residuals" should you compute, and to which distribution would you refer them?

  comment

• A2.12

  Computational Statistics and Statistical Modelling

  Part II, 2003

  (i) Suppose $Y_{1}, \ldots, Y_{n}$ are independent Poisson variables, and

  $$\mathbb{E}\left(Y_{i}\right)=\mu_{i}, \quad \log \mu_{i}=\alpha+\beta t_{i}, \quad \text { for } \quad i=1, \ldots, n,$$

  where $\alpha, \beta$ are two unknown parameters, and $t_{1}, \ldots, t_{n}$ are given covariates, each of dimension 1. Find equations for $\hat{\alpha}, \hat{\beta}$, the maximum likelihood estimators of $\alpha, \beta$, and show how an estimate of $\operatorname{var}(\hat{\beta})$ may be derived, quoting any standard theorems you may need.

  (ii) By 31 December 2001, the number of new vCJD patients, classified by reported calendar year of onset, were

  $$8,10,11,14,17,29,23$$

  for the years

  $$1994, \ldots, 2000 \text { respectively }$$

  Discuss carefully the (slightly edited) $R$ output for these data given below, quoting any standard theorems you may need.

  year

  year

  [1] 1994199519961997199819992000

  $>$ tot

  [1] $\begin{array}{lllllll}8 & 10 & 11 & 14 & 17 & 29 & 23\end{array}$

  first.glm - glm(tot year, family = poisson)

  $>\operatorname{summary}$ (first.glm)

  Call:

  glm(formula $=$ tot year, family $=$ poisson $)$

  Coefficients

  Estimate Std. Error z value $\operatorname{Pr}(>|z|)$

  (Intercept) $-407.8128599 .35366-4.1054 .05 \mathrm{e}-05$

  year $\quad 0.20556 \quad 0.04973 \quad 4.1333 .57 e-05$

  (Dispersion parameter for poisson family taken to be 1)

  Null deviance: $20.7753$ on 6 degrees of freedom

  Residual deviance: $2.7931$ on 5 degrees of freedom

  Number of Fisher Scoring iterations: 3

  Part II 2003

  comment

• A4.14

  Computational Statistics and Statistical Modelling

  Part II, 2003

  The nave height $x$, and the nave length $y$ for 16 Gothic-style cathedrals and 9 Romanesque-style cathedrals, all in England, have been recorded, and the corresponding $R$ output (slightly edited) is given below.

  

  You may assume that $x, y$ are in suitable units, and that "style" has been set up as a factor with levels 1,2 corresponding to Gothic, Romanesque respectively.

  (a) Explain carefully, with suitable graph(s) if necessary, the results of this analysis.

  (b) Using the general model $Y=X \beta+\epsilon$ (in the conventional notation) explain carefully the theory needed for (a).

  [Standard theorems need not be proved.]

  comment

• A1.13

  Computational Statistics and Statistical Modelling

  Part II, 2004

  (i) Assume that the $n$-dimensional vector $Y$ may be written as $Y=X \beta+\epsilon$, where $X$ is a given $n \times p$ matrix of $\operatorname{rank} p, \beta$ is an unknown vector, and

  $$\epsilon \sim N_{n}\left(0, \sigma^{2} I\right)$$

  Let $Q(\beta)=(Y-X \beta)^{T}(Y-X \beta)$. Find $\hat{\beta}$, the least-squares estimator of $\beta$, and state without proof the joint distribution of $\hat{\beta}$ and $Q(\hat{\beta})$.

  (ii) Now suppose that we have observations $\left(Y_{i j}, 1 \leqslant i \leqslant I, 1 \leqslant j \leqslant J\right)$ and consider the model

  $$\Omega: Y_{i j}=\mu+\alpha_{i}+\beta_{j}+\epsilon_{i j},$$

  where $\left(\alpha_{i}\right),\left(\beta_{j}\right)$ are fixed parameters with $\Sigma \alpha_{i}=0, \Sigma \beta_{j}=0$, and $\left(\epsilon_{i j}\right)$ may be assumed independent normal variables, with $\epsilon_{i j} \sim N\left(0, \sigma^{2}\right)$, where $\sigma^{2}$ is unknown.

  (a) Find $\left(\hat{\alpha}_{i}\right),\left(\hat{\beta}_{j}\right)$, the least-squares estimators of $\left(\alpha_{i}\right),\left(\beta_{j}\right)$.

  (b) Find the least-squares estimators of $\left(\alpha_{i}\right)$ under the hypothesis $H_{0}: \beta_{j}=0$ for all $j$.

  (c) Quoting any general theorems required, explain carefully how to test $H_{0}$, assuming $\Omega$ is true.

  (d) What would be the effect of fitting the model $\Omega_{1}: Y_{i j}=\mu+\alpha_{i}+\beta_{j}+\gamma_{i j}+\epsilon_{i j}$, where now $\left(\alpha_{i}\right),\left(\beta_{j}\right),\left(\gamma_{i j}\right)$ are all fixed unknown parameters, and $\left(\epsilon_{i j}\right)$ has the distribution given above?

  comment

• A2.12

  Computational Statistics and Statistical Modelling

  Part II, 2004

  (i) Suppose we have independent observations $Y_{1}, \ldots, Y_{n}$, and we assume that for $i=1, \ldots, n, Y_{i}$ is Poisson with mean $\mu_{i}$, and $\log \left(\mu_{i}\right)=\beta^{T} x_{i}$, where $x_{1}, \ldots, x_{n}$ are given covariate vectors each of dimension $p$, where $\beta$ is an unknown vector of dimension $p$, and $p<n$. Assuming that $\left\{x_{1}, \ldots, x_{n}\right\}$ span $\mathbb{R}^{p}$, find the equation for $\hat{\beta}$, the maximum likelihood estimator of $\beta$, and write down the large-sample distribution of $\hat{\beta}$.

  (ii) A long-term agricultural experiment had 90 grassland plots, each $25 \mathrm{~m} \times 25 \mathrm{~m}$, differing in biomass, soil pH, and species richness (the count of species in the whole plot). While it was well-known that species richness declines with increasing biomass, it was not known how this relationship depends on soil pH, which for the given study has possible values "low", "medium" or "high", each taken 30 times. Explain the commands input, and interpret the resulting output in the (slightly edited) $R$ output below, in which "species" represents the species count.

  (The first and last 2 lines of the data are reproduced here as an aid. You may assume that the factor pH has been correctly set up.)

  

  

  comment

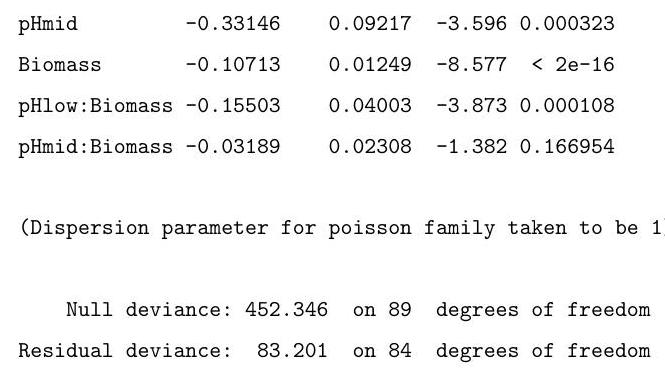
• A4.14

  Computational Statistics and Statistical Modelling

  Part II, 2004

  Suppose that $Y_{1}, \ldots, Y_{n}$ are independent observations, with $Y_{i}$ having probability density function of the following form

  $$f\left(y_{i} \mid \theta_{i}, \phi\right)=\exp \left[\frac{y_{i} \theta_{i}-b\left(\theta_{i}\right)}{\phi}+c\left(y_{i}, \phi\right)\right]$$

  where $\mathbb{E}\left(Y_{i}\right)=\mu_{i}$ and $g\left(\mu_{i}\right)=\beta^{T} x_{i}$. You should assume that $g()$ is a known function, and $\beta, \phi$ are unknown parameters, with $\phi>0$, and also $x_{1}, \ldots, x_{n}$ are given linearly independent covariate vectors. Show that

  $$\frac{\partial \ell}{\partial \beta}=\sum \frac{\left(y_{i}-\beta_{i}\right)}{g^{\prime}\left(\mu_{i}\right) V_{i}} x_{i}$$

  where $\ell$ is the log-likelihood and $V_{i}=\operatorname{var}\left(Y_{i}\right)=\phi b^{\prime \prime}\left(\theta_{i}\right)$.

  Discuss carefully the (slightly edited) $\mathrm{R}$ output given below, and briefly suggest another possible method of analysis using the function $\mathrm{glm}$ ( ).

  $>s<-\operatorname{scan}()$

  1: $\begin{array}{llllll}33 & 63 & 157 & 38 & 108 & 159\end{array}$

  7:

  Read 6 items

  $>r<-\operatorname{scan}()$

  1: 327172565065248688773520

  $7:$

  Read 6 items

  $>$ gender <- $\operatorname{scan}(, " \|)$

  1: b b b g g g

  $7:$

  Read 6 items

  $>$ age <- $\operatorname{scan}(, " \prime)$

  1: 13&under 14-18 19&over

  4: 13&under 14-18 19&over

  7 :

  Read 6 items

  $>$ gender <- factor (gender) ; age <- factor (age)

  $>\operatorname{summary}(\mathrm{glm}(\mathrm{s} / \mathrm{r} \sim$ gender $+$ age, binomial, weights $=\mathrm{r}))$

  Coefficients:

  

  Null deviance: $221.797542$ on 5 degrees of freedom

  Residual deviance: $0.098749$ on 2 degrees of freedom

  Number of Fisher Scoring iterations: 3

  comment